Table of contents
What is it?
The textbook definition of a bloom filter doesn't tell us much - A bloom filter is a space-efficient probabilistic data structure. But what does this mean? Instead of discussing a bloom filter's definition, it's more helpful to consider the problem it solves.
Let's imagine a scenario with a web server, a cache, and a client. The server maintains an extensive database of user profiles, and to expedite retrieval, it uses a caching system for frequently accessed profiles. Now, a cache is usually a highly efficient store of data. Its very purpose is to eliminate unnecessary database calls. But, as it always is with this intricate field of computer science, there's always a way to make the system more efficient. In this case, it's the number of cache misses and subsequent (expensive) database calls that occur. Let's see how bloom filters can reduce the number of cache misses here.
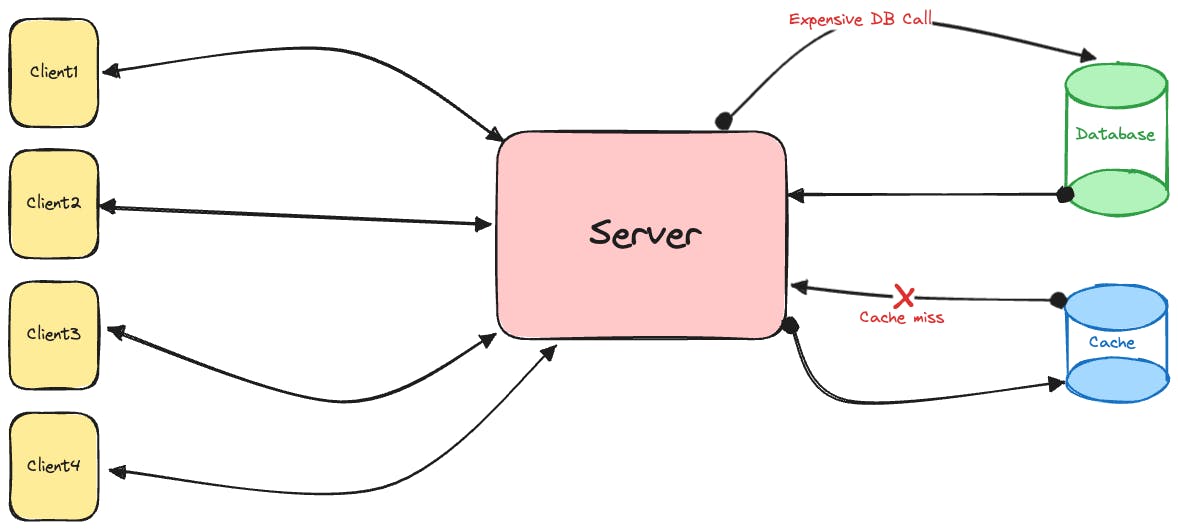
Bloom filters are like the unsung heroes of data structures, quietly tackling the classic dilemma of efficient membership queries in a vast sea of information. Using hash functions and a compact bit array (which we'll discuss in detail later), a Bloom filter provides a space-efficient probabilistic answer to the question: "Does this element belong to the set?" While it occasionally admits false positives, it never produces false negatives. This trade-off makes Bloom filters an ingenious solution for applications where speed and memory optimization are paramount, even if it means occasionally saying "maybe" instead of a definitive "yes."
Let's come back to our scenario now. The server, acting as the central hub, implements a Bloom Filter that encapsulates the unique identifiers (such as user IDs or usernames) of the profiles currently residing in the cache. When a client requests a specific user profile, the server first consults the Bloom filter. If the filter suggests that the profile might be in the cache, the server checks the cache directly. If the Bloom filter indicates a negative result, the server fetches the data from the main database. On the client side, requests are made without the need for direct cache queries unless the Bloom filter hints at a potential match. This way, the server significantly reduces the number of unnecessary cache requests by leveraging the space-efficient Bloom filter for quick, preliminary membership checks. While false positives may occasionally occur, the gains in speed and resource efficiency make Bloom filters an elegant solution for optimizing server-client interactions in scenarios involving cached data.
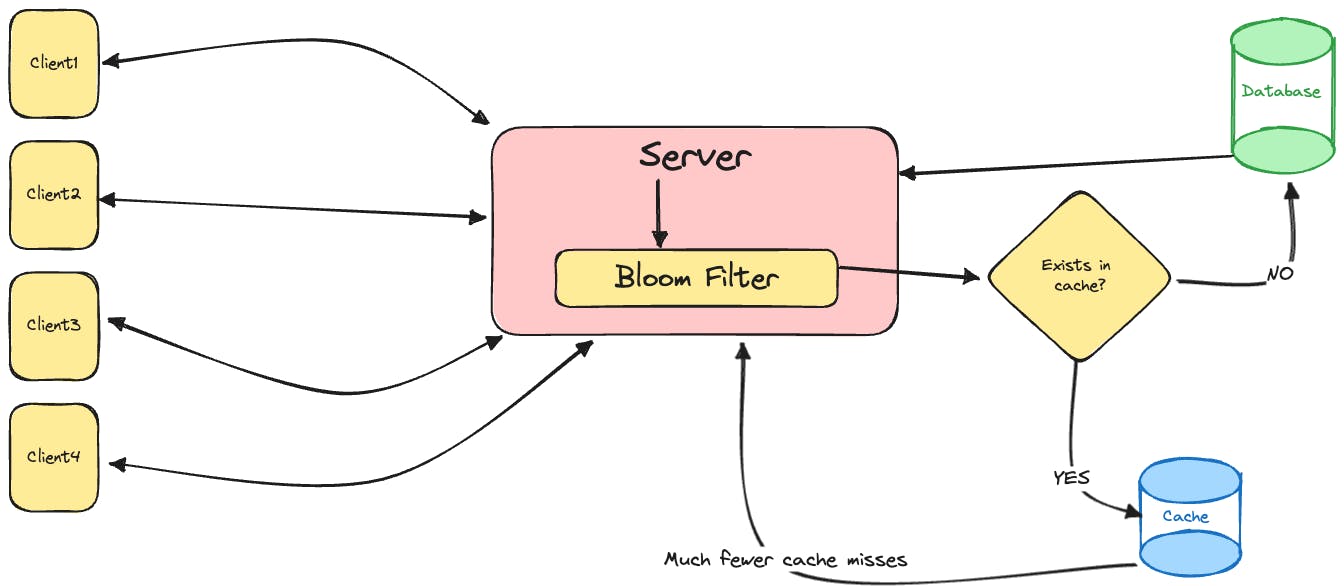
Now that we know what kind of a problem Bloom filters can solve, let's try to define it again.
A bloom filter is a probabilistic data structure that is used to check whether an element belongs to a set or not.
How Does it Work?
The definition must seem clearer now that you've seen how a Bloom Filter might be used in action, but a few murky words are still lurking. Let's see how a bloom filter works internally.
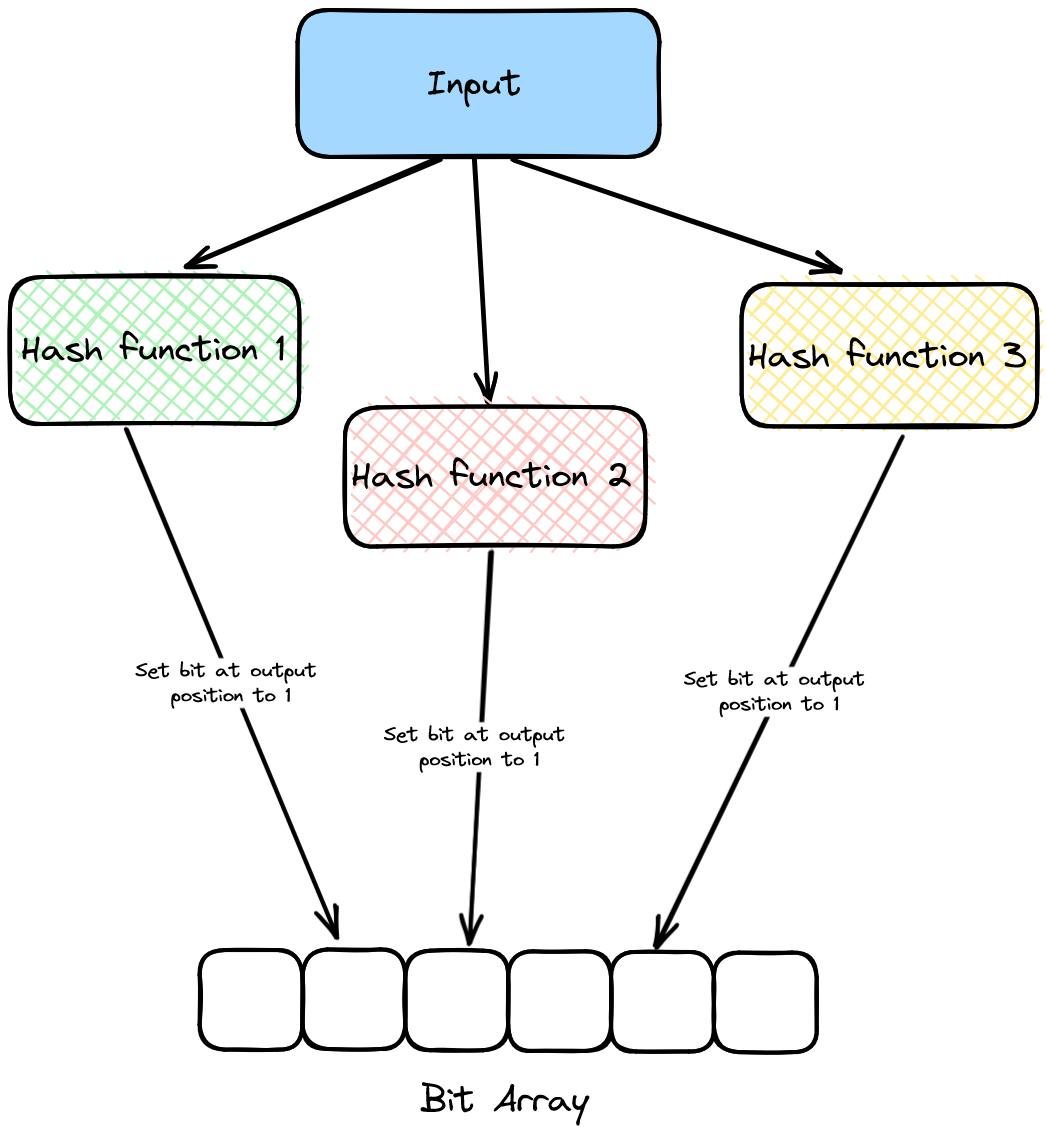
The definition states that a bloom filter is a probabilistic data structure. Sounds scary, but in reality, a bloom filter is just an array, not even an integer or character array, just a bit array, which means that each element of this array is either a 0 or a 1. What makes an array of 0s and 1s probabilistic? That answer lies behind how insertions occur in a Bloom Filter.
Returning to our earlier example, the server stores the most frequently accessed user profiles in the bloom filter. Let's say the unique identifier for each profile is the username, which is then encoded in the bloom filter. How does this encoding occur? The bloom filter uses hash functions. If you're unfamiliar with the concept of hash functions, you can read this article.
Let's take an example. For simplicity, we'll be using a naive modulo hash function defined as follows:
f(x:string) = len(x) % 10
So, the results returned by this hash function will always be between 0 and 9 (inclusive). The bloom filter bit array is initialized with all indexes set to 0. The indices obtained by applying the hash function to each inserted element are set to 1.
Let the list of most frequently searched usernames be ["Luna12", "SpecterX", "WhisperingSoul", "Quasar9", "MysticJourney"]. Let's see how each username will be inserted into the bloom filter.
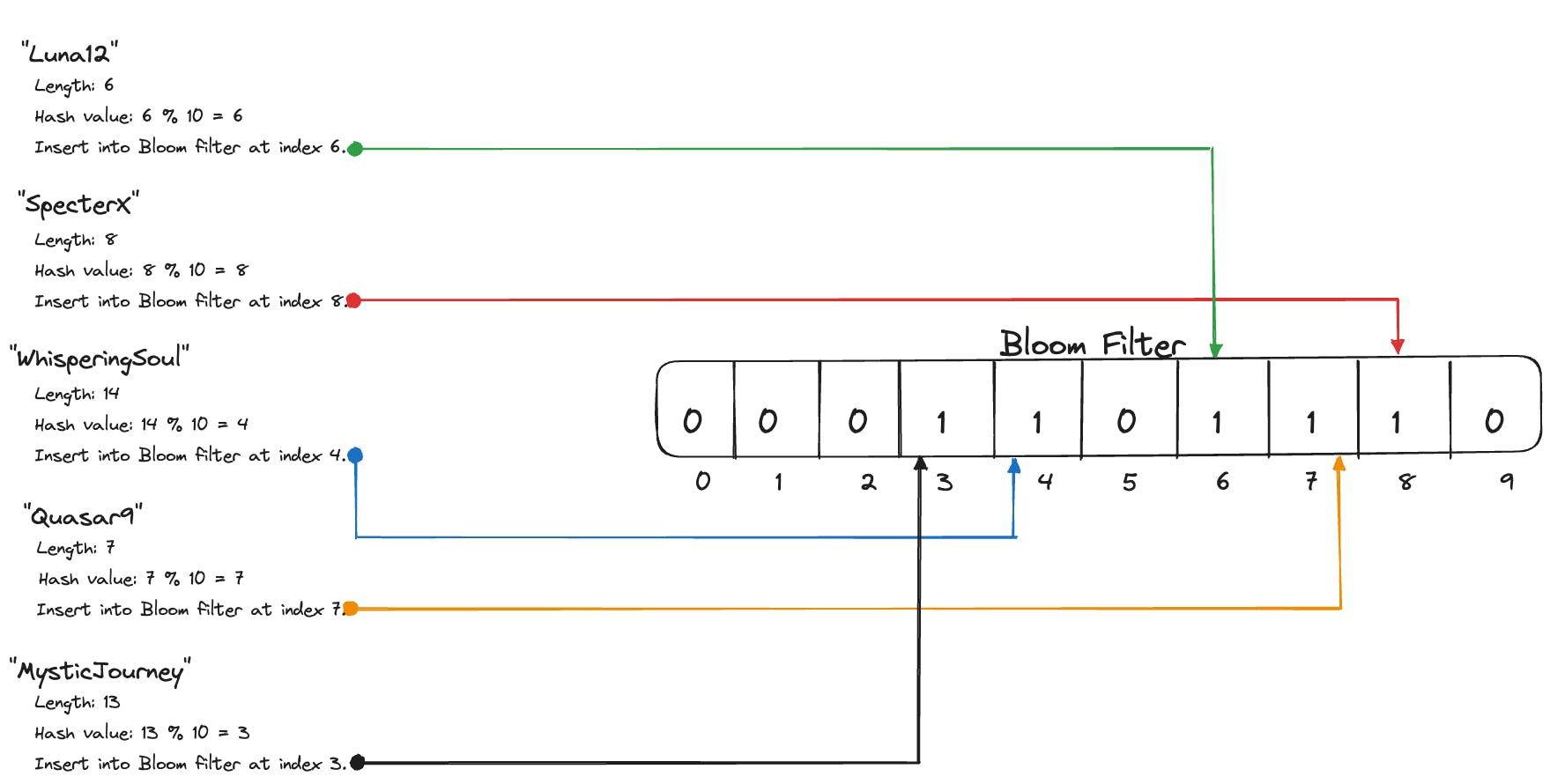
Thus, the indices 6, 8, 4, 7, and 3 of the bloom filter bit array are set to 1. Now that we know how an element is inserted into a bloom filter, we can explore how it performs a membership check!
Let's say the server gets an array of usernames whose membership it needs to check: ["SpecterX", "Quasar999", "Luna13"].
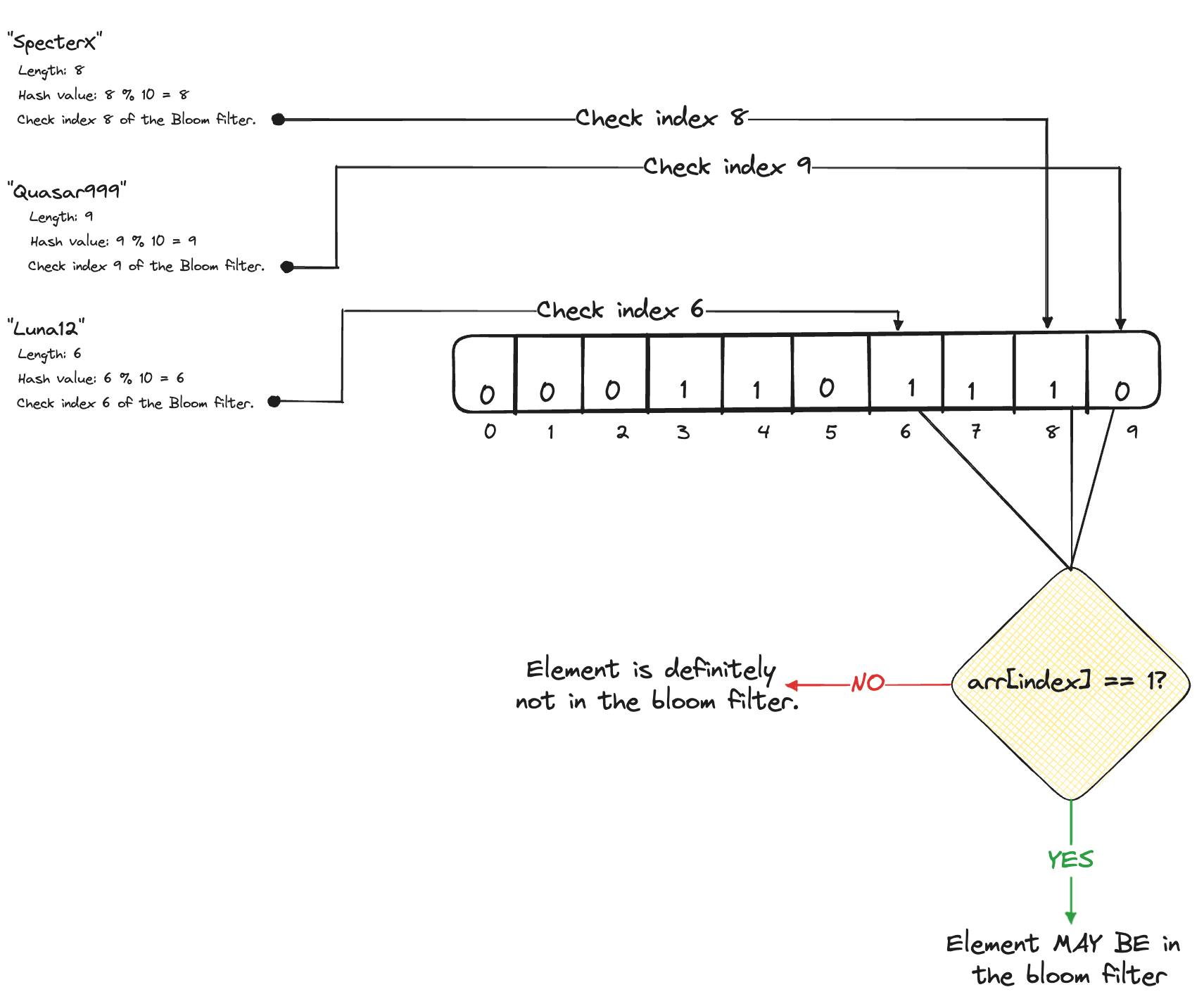
Let's dig a little deeper into the above diagram. As is expected, the username "SpecterX" is found in the bloom filter as the bit at index 8 is set to 1. The username "Quasar999" is however not found, because the bit at index 9 is set to 0.
These two examples are pretty self-explanatory, however, something very interesting happens in the third example. The bloom filter does not contain the username "Luna12", but the membership test suggests that it does. This phenomenon is referred to as a false positive, which means that even though an element might not be present in a bloom filter, it might appear as though it does. But, a very important point to be noted is that a bloom filter will never produce a false negative; that is, if the membership test suggests that an element is not in the bloom filter, it is guaranteed that the element is indeed not in the membership set.
The number of false positives that a bloom filter outputs is one of the factors on which its effectiveness is judged. In real-world applications, bloom filters usually employ multiple hash functions to encode the values that are to be stored. When inserting an element, all the available hash functions are applied individually to the input, and the output bit position of each hash function is set to 1.
To realize acceptable values of the false positive rate, fr, three parameters can be adjusted:
the length of the bloom filter array,
m,the number of employed hash functions,
k,the number of elements in the set,
n.
Theoretically, the lower bound of the false positive rate in a bloom filter is defined as:
$$f_r = \left(1 - e^{-\frac{kn}{m}}\right)k$$
Given this formula, the optimal value of k can be derived as:
$$k_{\text{opt}} = \frac{9m}{13n}$$
This formula can come in handy when you need to choose the optimal parameters for your bloom filter depending on your application.
Where is it used?
The example we discussed in the introduction is a very naive application of a bloom filter. However, in the real world, there are a plethora of uses for bloom filters. Their ability to provide quick and memory-efficient probabilistic membership tests makes them invaluable in scenarios where optimizing data retrieval and minimizing computational costs are paramount.
Network Routing and Forwarding Tables: In computer networking, bloom filters find applications in optimizing routing and forwarding tables. Traditional routing tables can become large and resource-intensive, especially in routers that need to handle vast amounts of network traffic. By using bloom filters to represent subsets of routing information, routers can efficiently check whether a destination IP address is within a particular routing prefix. This aids in quick decision-making during the forwarding process, allowing routers to handle high-speed packet forwarding with reduced memory requirements. The use of Bloom filters in network routing contributes to improved scalability and performance in large-scale network environments.
Web Caching and Content Delivery Networks (CDNs): Bloom filters find extensive use in web caching and Content Delivery Networks (CDNs) to optimize content retrieval and reduce latency. By storing frequently accessed items, such as web pages, in a Bloom filter, systems can quickly determine whether a requested item is likely to be in the cache. This helps in avoiding expensive disk or network fetches for content that is not present, thereby improving the overall performance of web applications. The compact nature of Bloom filters makes them particularly suitable for efficiently managing large sets of URLs or content identifiers.
Search Engine Indexing: Bloom filters are employed in search engine indexing to improve the speed and efficiency of query processing. In the vast indexes maintained by search engines, Bloom filters help identify whether a specific term or keyword is present in the index. This allows search engines to quickly eliminate irrelevant documents from consideration during a search query, streamlining the retrieval of relevant results. The use of Bloom filters in search engine indexing contributes to faster search responses and reduced computational overhead, enhancing the overall user experience in information retrieval. For more details on how Google uses bloom filters in its search engine, you can check out this video.
Conclusion
In the realm of data structures, Bloom filters stand out as a powerful and versatile tool, demonstrating their prowess across a spectrum of real-world applications. As we've explored the efficiency and ingenuity behind Bloom filters, it's evident that these compact structures offer elegant solutions to challenges in diverse domains.
In essence, Bloom filters exemplify the beauty of simplicity coupled with profound effectiveness—a testament to the impact that a well-designed data structure can have on the way we manage and retrieve information.
In the next article, I'll be demonstrating how you can implement a bloom filter yourself and make a neat little project out of it, so stay tuned!

