Shortest Path with Alternating Colors

Hello and welcome back to the Leetcode daily series! Today we'll be solving a mind-numbingly horrifying problem and of course, it involves graphs.

\Sigh\

Let's begin, shall we?

Understanding The Problem

Take a look at the given problem statement.

You are given an integer n, the number of nodes in a directed graph where the nodes are labeled from 0 to n - 1. Each edge is red or blue in this graph, and there could be self-edges and parallel edges.

You are given two arrays redEdges and blueEdges where:

redEdges[i] = [ai, bi] indicates that there is a directed red edge from the node ai to node bi in the graph, and

blueEdges[j] = [uj, vj] indicates that there is a directed blue edge from the node uj to node vj in the graph.

Return an array answer of length n, where each answer[x] is the length of the shortest path from the node 0 to node x such that the edge colors alternate along the path, or -1 if such a path does not exist.

Example 1:
Input: n = 3, redEdges = [[0,1],[1,2]], blueEdges = []
Output: [0,1,-1]
Example 2:
Input: n = 3, redEdges = [[0,1]], blueEdges = [[1,2]]
Output: [0,1,2]

Take your time to read through the problem statement, it's a little complicated.

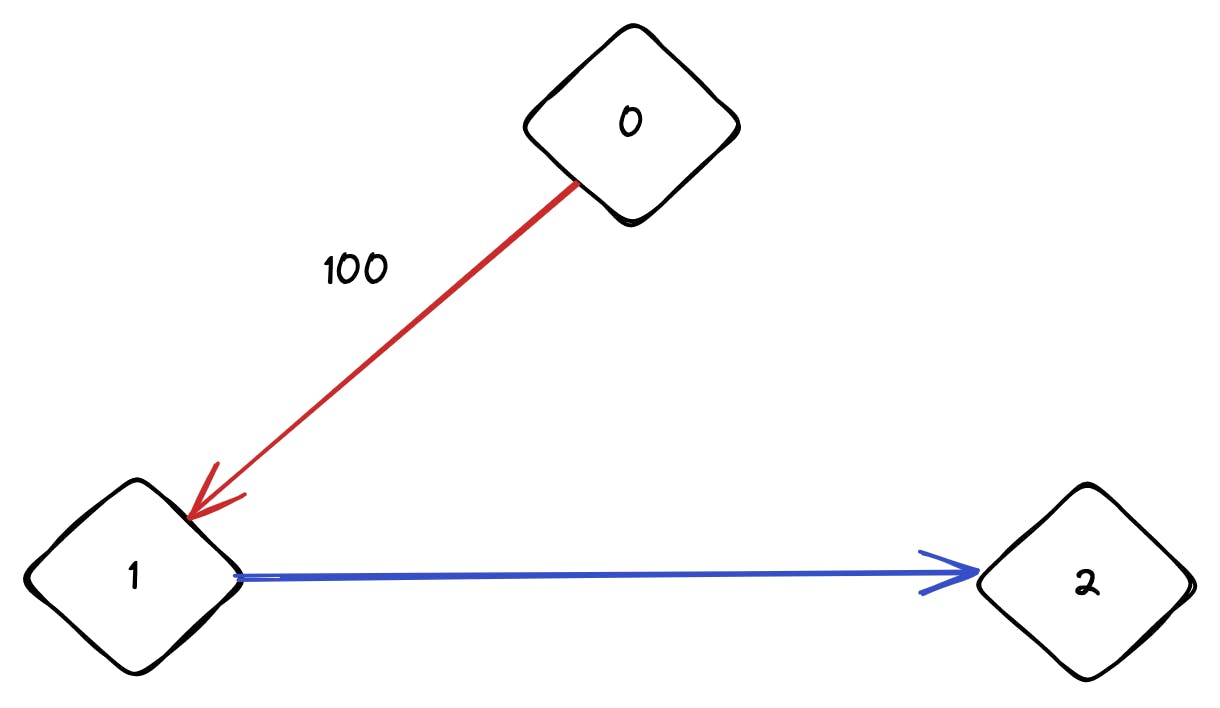
Look at the graph below that corresponds to the second example to get a better understanding of the problem. Here, the shortest distance with alternating edges from node 0 to node 1 is 1 and from node 0 to node 2 is 2.

Let's see how we can tackle this problem.

Intuition

First, we need to build an accessible representation of the given graph. For any given graph problem, an adjacency list works wonders in most cases. But here, we have two different kinds of edges: red and blue. Since we have a constraint in the given problem that the shortest path should have alternating red and blue edges, we need to keep track of the kinds of edges connecting different nodes too.

So, each element in the adjacency list should store three pieces of information:

Source node
Destination node
Kind of edge(red or blue)

Now that we have a suitable representation of the graph, we can think about what kind of traversal we need to follow in order to solve this problem.

Whenever a question requires us to find the shortest path in an unweighted graph, a breadth-first search is a good algorithm for it since in BFS, the first time a node is reached during a traversal, it is reached in the minimum possible steps from the source. The BFS algorithm does a level-wise iteration of the graph, that is, it reaches all the neighbors of the current node in the same step.

If you need a refresher on how BFS is implemented, you can find a good one here.

The only additional constraint in this problem is that the shortest path should also have alternating edges. So, in the queue that we maintain to keep track of the nodes on the same level, we also keep track of the kind of edge used to reach that node and the number of steps taken to reach that node.

We only push a new node to the queue if the color of the edge used to reach it is different from the previous edge on that path.

We also maintain an answer array to keep track of the number of steps taken to reach each node from node 0.

With this algorithm in your mind, try writing up a solution for this before moving on to the next section.

Coding Up The Solution

Here is the full C++ solution to this problem.

class Solution {
public:
    vector<int> shortestAlternatingPaths(int n, vector<vector<int>>& redEdges, vector<vector<int>>& blueEdges) {
        vector<vector<pair<int,int>>> adjList(n);
        for(auto edge : redEdges){
            adjList[edge[0]].push_back({edge[1],0});
        }

        for(auto edge : blueEdges){
            adjList[edge[0]].push_back({edge[1],1});
        }

        vector<int> answer(n,-1);

        queue<vector<int>> q;
        vector<vector<bool>> visit(n,vector<bool>(2));

        // queue element is of the form : [node,steps taken so far to reach that node,color of the prev edge]
        // 0 for red, 1 for blue
        q.push({0,0,-1});
        visit[0][1] = visit[0][0] = true;
        answer[0] = 0;

        while(!q.empty()){
            auto ele = q.front();
            q.pop();
            int node = ele[0], steps = ele[1], prevColor = ele[2];

            for(auto &[neighbor,color] : adjList[node]){
                if(!visit[neighbor][color] and prevColor != color){
                    visit[neighbor][color] = true;
                    q.push({neighbor,steps+1,color});
                    if(answer[neighbor] == -1) answer[neighbor] = steps + 1;
                }
            }
        }
        return answer;
    }
};

That's it for today! Hope you didn't find this problem too confusing.

Please consider subscribing to my newsletter to receive all my articles right in your inbox.

Cheers!

Shortest Path with Alternating Colors

Table of contents

Understanding The Problem

Intuition

Coding Up The Solution