Hello and welcome back to the Leetcode daily series! Today's problem is a very intriguing one. It covers scary-sounding topics such as binary tree traversals and recursion.
Take a look at the problem described below:

Once we understand the definition of a path, the rest of the problem is pretty straightforward. We need to find the maximum path sum of any non-empty path in the binary tree. An important thing to note here is that a path doesn't necessarily mean one that starts at a node and only traverses downwards to its children.
For example, in the below-given tree, a path can start at node 15 and go through node 20 to node 7.
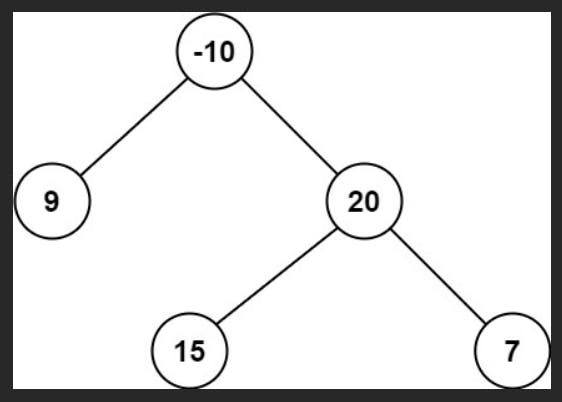
Understanding the Problem
The first solution that comes to mind is to traverse all possible paths in the given binary tree and return the maximum cost from them. For a binary tree with N nodes, the time complexity of this brute-force approach would be O(N^2).
This is not an ideal solution to this problem.
Let's break down the problem into parts. Let's say we're at a particular node A. Now, if we need the maximum path sum through node A, what would that be?
$$maxPathSum = val(A) + max(leftPathsSum) + max(rightPathsSum)$$
Intuition
So, what we need to do is apply this formula to every node in the tree, and the maximum of all these paths will be the answer to the problem.
While traversing through every node, we consider it to be the curving point for that particular path. So, the path sum for that particular node will be the sum of its left subtree's maximum path sum, its right subtree's maximum path sum and its value.
If this seems a little confusing, try doing a dry run with the code in the section below.
Coding up the Steps
The helper function that performs the DFS while also keeping track of the maximum path sum is given below:
int helper(TreeNode* root,int &ans){
if(!root) return 0;
int leftsum = max(0,helper(root->left,ans));
int rightsum = max(0,helper(root->right,ans));
ans = max(ans,(leftsum + rightsum + root->val));
return max(leftsum,rightsum) + root->val;
}
Let's try to understand this function line by line. The first line is of course the break condition for the recursion. If the node passed to the function is NULL, it returns 0.
Now, the next two lines are where all the magic happens.
We calculate the path sum of the left and right subtrees of the given node. To picture how this function returns this value, picture the edge case.
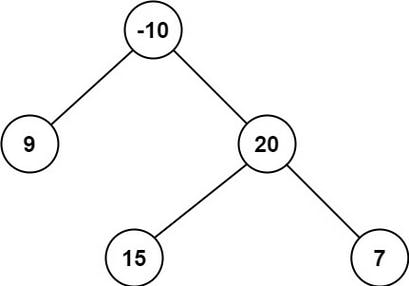
Imagine the leaf node with value 9 is passed to this function. The left and right sums for this iteration would be 0. Therefore the returned value to node -10 will be 9 itself. This is the maximum path sum that can be achieved once we move to the left child from node -10.
Similarly, nodes 15 and 7 will return their respective values to node 20. Now, what value will node 20 return to node -10? Pay attention to the part max(leftsum,rightsum) + root->val.
Thus, node 20 chooses the maximum of 15 and 7, that is 15, adds it to its value and returns the sum to node -10. Thus node -10 receives a value of 35 from node 20.
Node -10 itself will choose the maximum of 9 and 35, add that to its value and return it to the main function.
However, this is not the value that gives us the final answer because of one simple fact. If you remember the definition of a path, it can start at a child node, travel through a parent, and then to other child or parent nodes.
So, we need to keep track of this value within the same function.
ans = max(ans,(leftsum + rightsum + root->val));
In this line, we're updating the ans variable as the maximum of itself and the sum of the leftsum, rightsum and the node value.
This is where we consider the current node we're on as the curving point of the path. The value of (leftsum + rightsum + root->val) gives the path sum with the current node as the curving point. If this value is greater than ans, we assign it to ans.
One last point, why do we assign the maximum of 0 and the returned value from the helper function to leftsum and rightsum? Leave the answer in the comments if you can figure it out!
Putting Everything Together
The full solution to this problem is as follows:
class Solution {
public:
int helper(TreeNode* root,int &ans){
if(!root) return 0;
int leftsum = max(0,helper(root->left,ans));
int rightsum = max(0,helper(root->right,ans));
ans = max(ans,(leftsum + rightsum + root->val));
return max(leftsum,rightsum) + root->val;
}
int maxPathSum(TreeNode* root) {
int ans = INT_MIN;
helper(root,ans);
return ans;
}
};
This code will give us the maximum path sum of any given binary tree.
That's it for day 2 of this series, hope you had fun! Please leave any suggestions or feedback you might have in the comments.
Cheers!
