Hello and welcome back to yet another edition of the Leetcode Daily series! Today, we'll be looking at a problem that I honestly hated looking at. Graphs really do make me want to bang my head against a wall.

On that note, let's begin!

Understanding The Problem

Let's see the problem statement first.

There are n cities connected by some number of flights. You are given an array flights where flights[i] = [from<sub>i</sub>, to<sub>i</sub>, price<sub>i</sub>] indicates that there is a flight from city from<sub>i</sub> to city to<sub>i</sub> with cost price<sub>i</sub>.

You are also given three integers src, dst, and k, return the cheapest price from src to dst with at most k stops. If there is no such route, return -1.

This can seem a bit confusing without some visuals, so let me help you out with some examples.

Input: n = 4, flights = [[0,1,100],[1,2,100],[2,0,100],[1,3,600],[2,3,200]], src = 0, dst = 3, k = 1

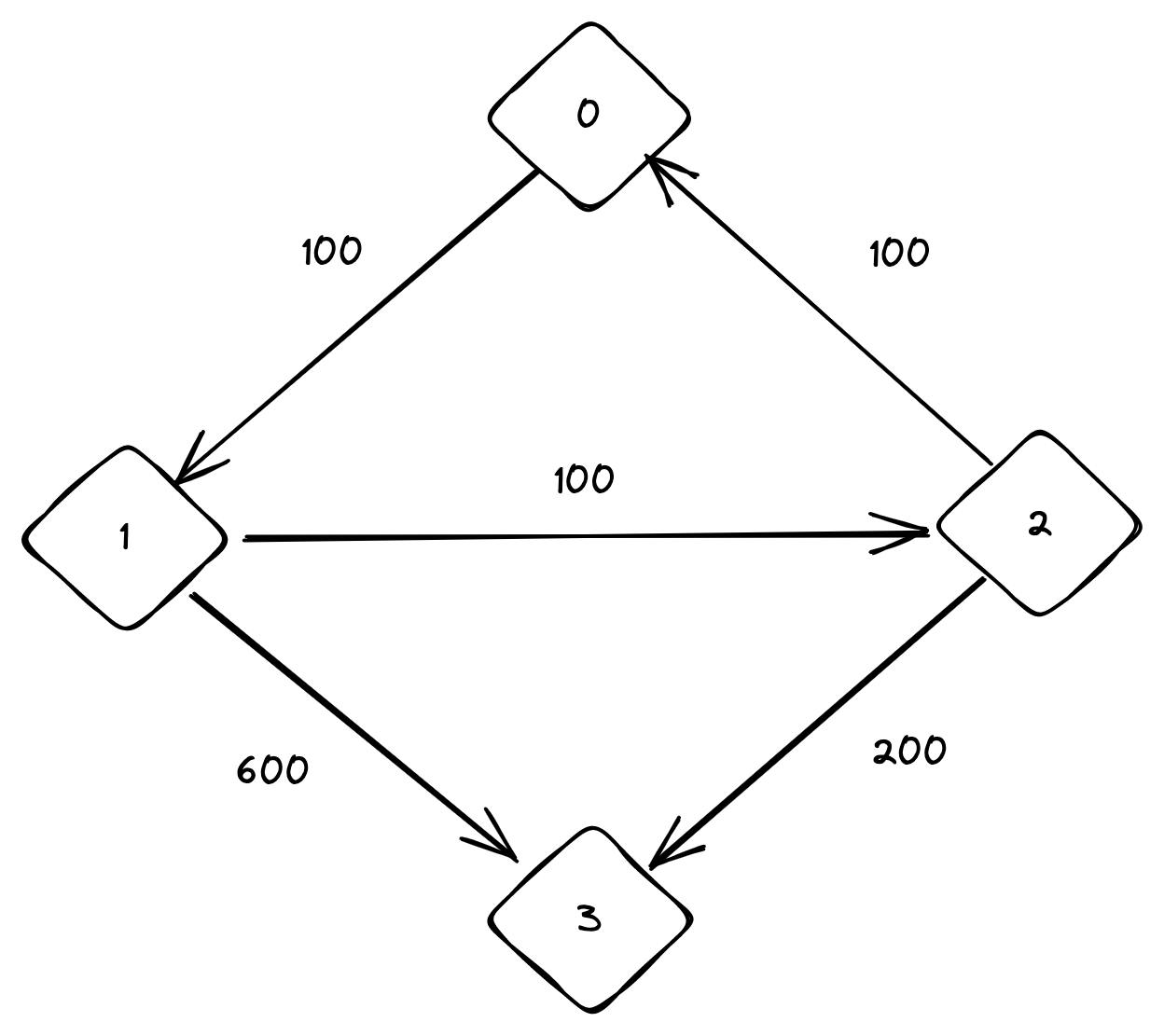
In the above example, first try to understand how we've constructed a graph from the given input. Each array inside flights is of the form [from, to, cost], so [0, 1, 100] signifies an edge from the node 0 to the node 1 which has a cost of 100.

We need to travel from node 0 to node 3 with at most one stop on the way. Try to solve this problem manually.

If you've come up with a cheapest cost of 700, you're right. The path we'll be following is from node 0 to node 1, and then from node 1 to node 3, which will have a total cost of 100 + 600 = 700 .

Notice that another path 0->1->2->3 is available to us at a cheaper cost, but that would require us to take two stops, which violates the constraint given.

Now that you have a better understanding of the problem, let's see the intuition behind this problem.

Intuition

The first thing we should look at is constructing a graph out of the given input. We'll be using an adjacency list representation for this. But, since each edge has a cost associated with it, we will need to store these costs as well.

Next, let's look at how we can find the least cost path between two nodes, with a constraint on the length of the path.

For an unweighted graph, a regular breadth-first search algorithm would suffice to find the shortest path. If you're unfamiliar with the BFS algorithm, check out the links in the Further Reading section before proceeding ahead.

A very important property of BFS is that the first a node is reached during traversal, it is reached at the minimum distance from the source. But, for a weighted graph, since we need to consider the weight of each edge too, we can't use a regular BFS algorithm. The only way for BFS to find the shortest path in a weighted graph is to search the entire graph and keep recording the minimum distance from the source to the destination node. As you can imagine, this is not at all efficient.

But, since we can only take k stops on our path, our search space is limited to paths with lengths less than or equal to k . As a result, our efficiency is significantly improved.

In the BFS approach, we perform a level-wise iteration over the nodes. So, we first explore all the nodes at a distance of 1 from the source, and then move on to all the nodes at a distance of 2, and so on. As we move from a distance of one to two, we increase the number of stops to one. Since we're allowed a maximum of k stops, we can explore all nodes up to a distance of k+1.

Keeping this in mind, let's whip up an algorithm to solve this headache.

Algorithm

• Create an adjacency list where adj[i] will contain all the neighbors of node i and the corresponding price it takes to move to a neighbor.

• Initialize a dist array where dist[i] will store the minimum cost to reach a node from the src node. Initially, all indexes of this array should contain a large value, except for the src, which will have a value of 0.

• Initialize a queue storing {stops, node, distance} triplets. Initially, the queue will have only {0,src,0}.

• While the queue is not empty, do the following:

  • Pop the element in the front of the queue. If the stops for the popped element is greater than k, we can't pursue this path further. So, we can skip the rest of the steps in the loop and move on to the next element.

  • We iterate over the neighbors of the node popped from the queue. If the current cost plus the weight of the edge to this neighbor is less than the value stored in dist[neighbor] that is, the current cost to reach this node is less than the previous minimum, and the number of stops is less than or equal to k then:

    • We update dist[neighbor] to cost + weight.

    • We push {stops+1, neighbor, cost + weight} to the queue.

• Once we exit this loop, we check if the value of dist[dst] is equal to INT_MAX. If it is, then there is no path connecting the src to the dst with a length less than or equal to k + 1. In this case, we return -1. Otherwise, we return the value stored in dist[dst].

That's all there is to this problem (says the guy who took two hours to solve it). Try to code up this algorithm before moving on to the next section.

Coding Up The Solution

class Solution {
public:
    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
        vector<pair<int,int>> adj[n];
        for(auto it : flights){
            adj[it[0]].push_back({it[1],it[2]});
        }

        queue<pair<int,pair<int,int>>> q;
        q.push({0,{src,0}});
        vector<int> dist(n,1e9);
        dist[src] = 0;

        while(!q.empty()){
            auto it = q.front();
            q.pop();
            int stops = it.first;
            int node = it.second.first;
            int cost = it.second.second;

            if(stops > k) continue;

            for(auto iter: adj[node]){
                int adjNode = iter.first;
                int weight = iter.second;

                if(cost + weight < dist[adjNode] and stops <= k){
                    dist[adjNode] = cost + weight;
                    q.push({stops+1,{adjNode,cost+weight}});
                }
            }
        }

        if(dist[dst] == 1e9) return -1;
        return dist[dst];
    }
};

I'll see you back tomorrow with yet another frustrating problem to solve. Hope you had fun today.

Cheers!

Further Reading

• Breadth-First Search: https://www.geeksforgeeks.org/breadth-first-search-or-bfs-for-a-graph/