Hello and welcome back to the Daily Leetcode Series! We have a very interesting problem ahead of us today so let's dive in!

Understanding The Problem

Let's take a look at the problem description first:

You are given two strings of the same length s1 and s2 and a string baseStr.

We say s1[i] and s2[i] are equivalent characters.

• For example, if s1 = "abc" and s2 = "cde", then we have 'a' == 'c', 'b' == 'd', and 'c' == 'e'.

Equivalent characters follow the usual rules of any equivalence relation:

• Reflexivity: 'a' == 'a'.

• Symmetry: 'a' == 'b' implies 'b' == 'a'.

• Transitivity: 'a' == 'b' and 'b' == 'c' implies 'a' == 'c'.

For example, given the equivalency information from s1 = "abc" and s2 = "cde", "acd" and "aab" are equivalent strings of baseStr = "eed", and "aab" is the lexicographically smallest equivalent string of baseStr.

Return the lexicographically smallest equivalent string of baseStr by using the equivalency information from s1 and s2.

Seems kind of complex, doesn't it? Let's simplify it a bit.

First off, let's simplify the inputs we've been given.

1. Strings s1 and s2 : Forget about these two strings. Think in the terms of mappings. You've been given an equivalence mapping between different characters. That's it.

2. String baseStr : The string that you need to modify with the mappings given. The constraint is that it should be the lexicographically smallest string.

Now, the only decision that we need to make is how to store this mapping. A point to note here is that there is the transitivity property included in the equivalence relations. One solution to storing this kind of relationship would be a graph.

Intuition

Let's visualize how exactly this problem can be solved using graphs. We'll be representing characters as nodes, and the equivalence relations between these characters as edges between these nodes.

An important concept to be familiar with to solve this problem is that of a connected component.

A connected component of an undirected graph is a subgraph in which each pair of nodes is connected via a path. In a connected component, all nodes are reachable from each other.

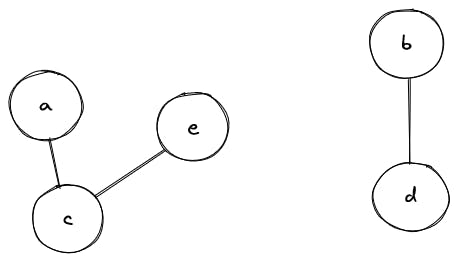
In the graph given above, there are two connected components. This graph corresponds to the example given above.

Let's see how we can solve this problem from these connected components.

The lexicographically smallest characters in these components are "a" and "b" respectively. So, in the baseStr we need to replace all occurrences of "c" and "e" with "a", and occurrences of "d" with "b". That's it!

Now, in order to find the lexicographically smallest character in each connected component of the graph, we can use the Depth First Search algorithm.

Coding Up The Solution

Here's the full solution to this problem.

class Solution {
public:

    void dfs(int node,vector<vector<int>>& adj,vector<int>& component,int &minchar,vector<int>& vis){
        //mark node as visited
        vis[node] = 1;

        //add current character to the connected component
        component.push_back(node);
        //if current character is the lexicographically smallest one in this connected component, then store it in minchar
        minchar = min(minchar,node);

        //recursively call dfs for each node in the connected component
        for(int i = 0;i < 26; i++){
            if(adj[node][i] and !vis[i]){
                dfs(i,adj,component,minchar,vis);
            }
        }
    }
    string smallestEquivalentString(string s1, string s2, string baseStr) {
        vector<vector<int>> adj(26,vector<int>(26,0));
        //create an adjacency matrix
        for(int i = 0; i < s1.size(); i++){
            adj[s1[i] - 'a'][s2[i] - 'a'] = 1;
            adj[s2[i] - 'a'][s1[i] - 'a'] = 1;
        }

        //create a mapping array for each character
        //a = "0", b = "1" etc
        vector<int> mappingChar(26,0);
        for (int i = 0; i < 26; i++) {
            mappingChar[i] = i;
        }

        vector<int> vis(26,0);

        for(int i = 0;i < 26; i++){
            //perform dfs on each character
            if(!vis[i]){
                int minchar = 27;
                vector<int> component;
                dfs(i,adj,component,minchar,vis);

                //for each character, map its value to the minchar in that connected component
                for(int vertex : component){
                    mappingChar[vertex] = minchar;
                }

            }
        }
        string ans;
        for(char c : baseStr){
            ans += (char)(mappingChar[c-'a'] + 'a');
        }
        return ans;
    }
};

That's it for today! Hope you like this solution. Please subscribe to my newsletter to be notified of all my new articles.

Cheers!