Hello and welcome to the daily Leetcode problem series. This is the first problem I'm posting the solution to and hope to continue making daily posts after solving each Leetcode daily problem for the foreseeable future.

The problem description is as follows:

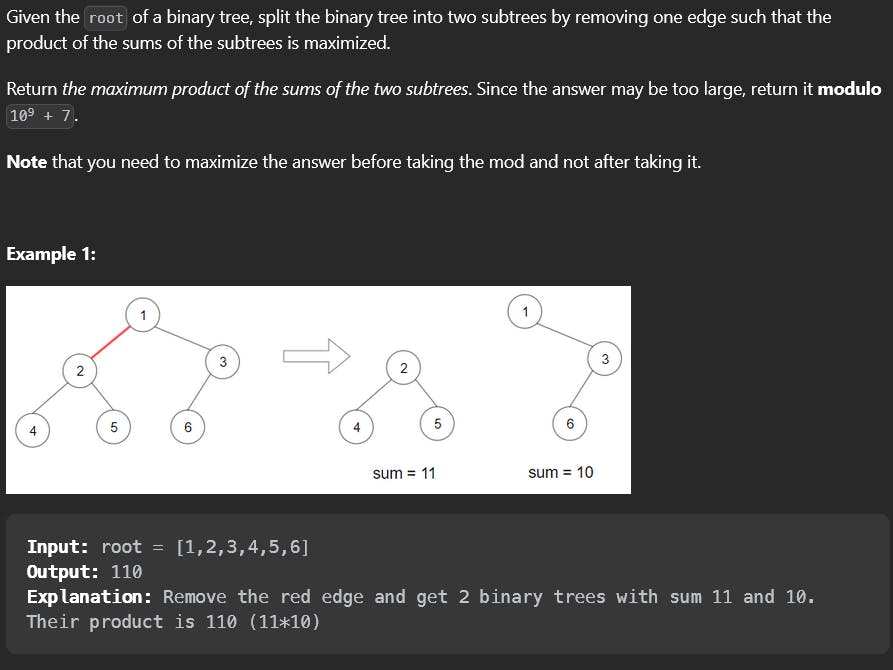
Understand the problem

The description is pretty simple: given a binary tree, we need to split it into two parts by removing at most one edge, such that the product of the sums of the individual subtrees is maximum.

Take a minute, and read the problem at least three times. That should be the first step whenever solving any competitive coding question. Read, read, and read. You don't want to be halfway through your allotted time limit and then realize that you missed an important detail in the question because you didn't read it thoroughly.

Intuition

So, what do we need to do? Let's break it down into steps:

1. Split the tree into two subtrees.

2. Calculate the sum of the individual subtrees and multiply them.

3. Repeat this process over all possible subtrees in order to calculate the maximum product.

The first thing that comes into mind when thinking about these steps is that we need to perform a traversal of the entire tree. A depth-first search would work like a charm in this scenario.

Now, how to get the sum of the remaining subtree when the current subtree is removed?

The easiest way to do this would be to first calculate the sum of the entire tree. This way, after calculating the sum of the current subtree, we can subtract that from the total sum to get the sum of the remaining subtree.

In short,

$$sumRemainingSubtree = totalTreeSum - currentTreeSum$$

So, we have our first objective: calculate the sum of the entire tree.

Coding Up The Steps

DFS comes to the rescue here again. The following function can be used to calculate the sum of the entire tree:

void getTotalSum(TreeNode* root){
     if(!root) return;
    //sum can be declared as a global variable
     sum += root->val;
     getTotalSum(root->left);
     getTotalSum(root->right);
}

This is a pretty straightforward use case of DFS with recursion.

Now, we need a function that can give us one more variable in Eq. 1 : the sum of the current subtree. In this function, we also need to update the final result as the sum of each subtree is calculated.

The following function can be used to do so:

int getSubtreeSum(TreeNode* root){
        if(!root) return 0;

        long long leftSum = getSubtreeSum(root->left);
        long long rightSum = getSubtreeSum(root->right);
        //update the final ans variable
        //(sum-leftsum) gives the sum of the right subtree
        //(sum-rightsum) gives the sum of the left subtree
        ans = max({ans,(sum - leftSum) * leftSum,(sum-rightSum) * rightSum});
        return leftSum + rightSum + root->val;
}

The getSubtreeSum function does the following:

• First, the break condition for the recursion. If the passed TreeNode is NULL, the function returns 0. This happens when a leaf node calls this function.

• Second, it calculates the sum of the left subtree and right subtree of the current node by calling itself.

• Third, and most importantly, the ans variable is updated as the maximum of

  • ans itself

  • (sum-leftSum) * leftSum

  • (sum - rightSum) * rightSum

Putting Everything Together

The final solution looks like this:

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    static const int MOD=1e9+7;
    long long ans = 0;
    long long sum = 0;
    void getTotalSum(TreeNode* root){
        if(!root) return;

        sum += root->val;
        getTotalSum(root->left);
        getTotalSum(root->right);
    }
    int getSubtreeSum(TreeNode* root){
        if(!root) return 0;

        long long leftSum = getSubtreeSum(root->left);
        long long rightSum = getSubtreeSum(root->right);
        ans = max({ans,(sum - leftSum) * leftSum,(sum-rightSum) * rightSum});
        return leftSum + rightSum + root->val;
    }
    int maxProduct(TreeNode* root) {
        getTotalSum(root);
        getSubtreeSum(root);
        return ans % MOD;   
    }
};

The code can be made even more concise by using only one function to calculate the sum of the entire tree and also the sum of the subtrees.

Hope you liked this explanation. Come back tomorrow for the solution to the next LeetCode daily.

Cheers!