Hello and welcome to day 4 of the daily Leetcode series! We have a very interesting problem ahead of us today so I hope you're ready to put a few of those brain cells to good use.

Understanding The Problem

Let's take a look at the problem description.

Given an n x n array of integers matrix, return the minimum sum of any falling path through matrix.

A falling path starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from the position (row, col) will be (row + 1, col - 1), (row + 1, col), or (row + 1, col + 1).

Reread the problem a few times. Then try to solve it for the below-given matrix manually.

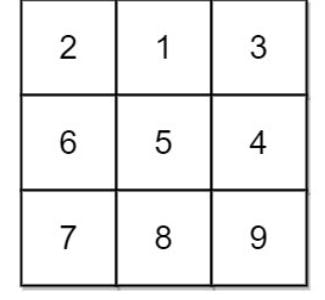
If you got the answer as 13, congratulations, you've understood the problem.

Now, let's think about how to go about solving this problem.

Intuition

The first clue when a problem like this is given is the quantity that we have to compute. Here, we need to find the minimum falling path sum. Pay attention to the word minimum. Whenever a problem asks us to find the minimum or maximum of some quantity, the first thought that should come into our head is dynamic programming.

The second clue for this problem is the choice that we need to make for each element in the matrix. Since we need to find the minimum path sum, for each element in the matrix, we need to choose whether or not to include it in our answer so that our chosen path goes through that element.

These two clues point us toward recursion and memoization.

I will be discussing three solutions to this problem:

1. Recursion

2. Recursion with memoization

3. Top-down approach

Recursion

There are two main steps involved in writing a recursive function.

The first step to coding a recursive solution to any problem is to figure out the base condition, i.e., the condition which would cause the recursive function to make an early return.

The second step is to code the choice diagram for the problem. A choice diagram chooses between two possible solutions by considering the given constraints and the quantity that needs to be optimized.

Let's start by thinking about what the parameters for the recursive function will be. From there, we can try to derive the base condition.

We need three parameters for the recursive function: the input matrix, the current row index, and the current column index. That's it!

Now, if we start from the first row, what would the base condition for the recursive function be?

Give the following code snippet a look.

int minFallingPathSum(vector<vector<int>>& matrix) {
        int ans = INT_MAX;
        int n = matrix.size(),m = matrix[0].size();
        for(int i = 0;i < m; i++){
            ans = min(ans,helper(matrix,0,i));
        }
        return ans;
}

This is where we call the recursive helper function for each element of the first row. We need to return the minimum path sum, so we assign the minimum of ans and helper(matrix,0,i) to ans.

Why do we call the helper function for each element of the first row? We consider each element of the first row as the starting point of the path and return the one which gives the minimum path sum.

Now that we have the caller function decoded, can you try and think of the base condition for the recursive function?

The recursive function will return only when we are at a position from which we can't travel any further. So, obviously, the base condition will be when the current row is the last row of the matrix. When we reach the last row of the matrix, we return the value of the current cell.

Once the base condition is decided, the second step is to code up the choice diagram. We need the minimum of the falling path sum, so we choose the minimum value of all the values from the paths.

Say we're at index (i,j) of the matrix. The next cells we could travel to are:

• (i+1,j-1) => diagonally left

• (i+1,j) => directly below

• (i+1,j+1) => directly right

We choose the minimum of these three values.

Try to code up the recursive function with the information available to you now. Once you've given it an honest effort, look at the code given below.

int helper(vector<vector<int>>& matrix,int i,int j){
        if(i == matrix.size()-1 and j < matrix[0].size() and j >= 0){
            return matrix[i][j];
        }
        //return INT_MAX in case of invalid index
        if(j >= matrix[0].size() or j < 0) return INT_MAX;

        return matrix[i][j] + min({helper(matrix,i+1,j-1),helper(matrix,i+1,j+1),helper(matrix,i+1,j)});
    }

That's it for the recursive approach. However, if you pay attention, this isn't that efficient of an approach since it has an exponential time complexity.

Recursion with Memoization

With just a few lines of code, we can improve the time complexity of this recursive approach. In the memoization approach, we store the results returned by the recursive function in a 2D matrix so that we don't recompute the answers for the same given input.

Try to code up this approach yourself before moving on to the code.

    int helper(vector<vector<int>>& matrix,
                int i,
                int j,
                vector<vector<int>>& dp)
{
        if(i == matrix.size()-1 and j < matrix[0].size() and j >= 0){
            return dp[i][j] = matrix[i][j];
        }
        if(j >= matrix[0].size() or j < 0) return INT_MAX;

        if(dp[i][j] != INT_MAX) return dp[i][j];

        return dp[i][j] = matrix[i][j] + min({helper(matrix,i+1,j-1,dp),helper(matrix,i+1,j,dp),helper(matrix,i+1,j+1,dp)});
}

    int minFallingPathSum(vector<vector<int>>& matrix){
        int ans = INT_MAX;
        int rows = matrix.size(),cols = matrix[0].size();

        vector<vector<int>> dp(rows,vector<int>(cols,INT_MAX));

        for(int i = 0;i < cols;i++){
            ans = min(ans,helper(matrix,0,i,dp));
        }
        return ans;
    }

As you can see, just adding a few lines of code makes it good enough to pass all test cases on any competitive coding platform.

Top-Down Approach

We can solve this problem without recursion as well. We build a 2D matrix from the top down in this approach.

First, initialize the first row of the dp matrix with the values of the first row of the input matrix.

This makes sense because, for each cell of the first row of the matrix, the minimum path sum will just be its own value.

Next, we iterate over each cell of the matrix starting from the second row. Three cases arise, depending on which column we're currently on.

1. First column (j = 0): Here we can't consider the value of the cell diagonally left because that would be out of bounds. So, we assign matrix[i][j] + min(dp[i-1][j],dp[i-1][j+1]) to dp[i][j].

2. Last column (j = cols -1): Here we can't consider the value of the cell diagonally right because that would be out of bounds. So, we assign matrix[i][j] + min(dp[i-1][j-1],dp[i-1][j]) to dp[i][j].

3. Any column in between (j > 0 and j < cols-1): Here we consider all three possible sources and assign the minimum of those to dp[i][j] as matrix[i][j] + min({dp[i-1][j-1],dp[i-1][j],dp[i-1][j+1]}) .

 int minFallingPathSum(vector<vector<int>>& matrix){
        int rows = matrix.size(), cols = matrix[0].size();

        vector<vector<int>> dp(rows,vector<int>(cols,INT_MAX));

        for(int i = 0;i < cols; i++){
            dp[0][i] = matrix[0][i];
        }

        for(int i = 1;i < rows; i++){
            for(int j = 0; j < cols; j++){
                if(j == 0 and j + 1 < cols){
                    dp[i][j] = matrix[i][j] + min(dp[i-1][j],dp[i-1][j+1]);
                }

                if(j == cols-1 and j-1 >= 0){
                    dp[i][j] = matrix[i][j] + min(dp[i-1][j],dp[i-1][j-1]);
                }

                if(j-1 >= 0 and j+1 < cols){
                    dp[i][j] = matrix[i][j] + min({dp[i-1][j-1],dp[i-1][j],dp[i-1][j+1]});
                }
            }
        }
        return *min_element(dp[rows-1].begin(),dp[rows-1].end());
    }

Finally, we get our answer by selecting the minimum element from the last row of the dp matrix.

That's it for today! Hope you had fun learning all these new approaches to this problem.

Come back tomorrow for yet another dive into the fascinating world of problem-solving.

Cheers!